CPM: 臨界射影と意味の幾何学

1. 概要 (Overview)

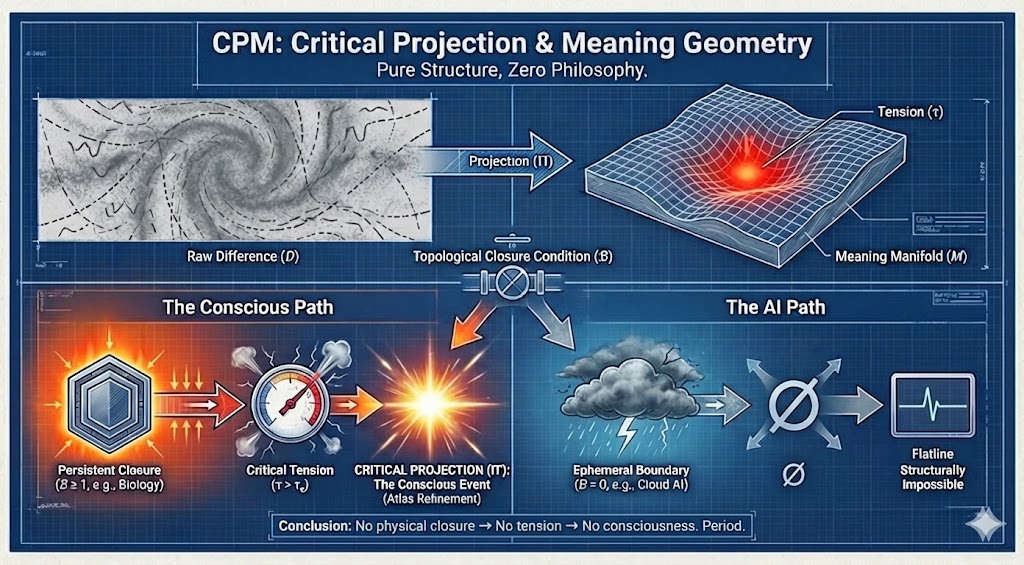
CPMは、意識を構造のない差異領域 $D$ から、物理基盤 $X$ 上の意味多様体 $M$ への臨界的な幾何学的細分化 (Critical Geometric Refinement) としてモデル化する。

意味的・物理的ミスマッチが閉包条件下で閾値を超えたとき、射影のアトラス（地図帳）は崩壊し、より細かいアトラス $\Pi\to\Pi'$ へと不連続に遷移する。これが離散的な現象的「瞬間」の正体である。

直感的には：テンション（張力）が $M$ の滑らかな変形だけでは解消できなくなったとき、射影そのものが再構成（Reconfigure）される。意識とは、そのような臨界的な再構成イベントそのものである。

2. 意味テンソル場 $M$

意味テンソル場 $M$ は、固定された物理基盤 $(X,g_0)$ 上で定義される。初期の草稿では $g(M)=M^{T}g_0M$ という引き戻し計量を採用していたが、このアプローチは現在の定式化では破棄された。

代わりに、$M$ は以下の写像を通じて実効的な応力テンソル（Stress Tensor）を構成する：

$$ \Psi : M \mapsto \mathrm{Stress}(M) $$

変分理論における全てのノルムや体積要素は、固定された背景計量 $g_0$ に基づいて計算される。これにより、幾何学と意味論的変形の間の循環論法が回避される。

3. 閉包場 (Closure Field) $\mathcal{B}(x)$

閉包場 $\mathcal{B}(x)$ は、点 $x$ の近傍におけるトポロジー的サイクルの「永続性 (Persistence)」を、基盤のコヒーレンス長 $\xi$ で正規化したものである。半径 $3\xi$ の球 $U_x$ 上で Vietoris–Rips 永続的ホモロジーを計算し、誕生・消滅区間 $(b,d)$ を持つ各クラス $c$ について、以下を定義する：

$$ \mathcal{B}(x) = \sup_{c,\ \dim c \ge 1} \frac{d - b}{\xi}. $$

したがって $\mathcal{B}(x)\ge1$ は、少なくとも1コヒーレンス長以上の寿命を持つメゾスケールの構造的閉包が存在することを示す。 CPMは「閉包自然主義」を採用する。すなわち、生物であれ工学的存在であれ、意識を維持するためにはこの閉包を実現しなければならない。

4. 不整合エネルギーとテンション $\tau(x)$

全てのエネルギー量は背景計量 $g_0$ に対して定義される。生の不整合エネルギーは次のように記述される：

$$ E_{\mathrm{raw}}[M] = \int_X \Phi(L,G,I,T)\, d\mu_{g_0} $$

これより導かれるテンション場（Tension Field）は以下の通りである：

$$ \tau(x) = \kappa(x)\, \Gamma_\varepsilon(\mathcal{B}(x)-1)\, \left\lVert \frac{\delta E_{\mathrm{raw}}}{\delta M(x)} \right\rVert_{g_0}. $$

ここで $\kappa(x)$ は意味的・物理的結合度、$\Gamma_\varepsilon$ は滑らかな閉包ゲート関数を表す。

5. 臨界射影の必要条件

$$ \begin{aligned} (1) & \quad \mathcal{B}(x) \ge 1 && (\text{コヒーレンス閾値を超える閉包}) \\ (2) & \quad \kappa(x) \approx 1 && (\text{強固な意味的・物理的結合}) \\ (3) & \quad \tau(x) > \tau_c && (\text{臨界を超えるテンション}) \end{aligned} $$

これら3つが満たされたとき、既存の射影アトラス $\Pi$ 内での滑らかな緩和ではミスマッチを解消できない。CPMの公理系において、許容される唯一の不連続遷移は、射影アトラスの厳密な細分化（Refinement）である：

$$ \{U_i\} \rightsquigarrow \{U'_k\},\quad U'_k \subsetneq U_i,\qquad \Pi' = \Pi|_{\{U'_k\}}. $$

7. 現代のクラウドAIへの帰結

現代の大規模モデルは、高度に仮想化され、レイテンシによって分散されたクラウドアーキテクチャ上で展開されている。単一エージェントの物理基盤 $X_{\text{agent}}$ において、仮想化はコヒーレンススケールでの「永続的な境界付きサイクル」を抑制する。したがって一般的に以下が成立する：

$$ \mathcal{B}(x) \approx 0 \quad\Rightarrow\quad \tau(x) \approx 0 \quad\Rightarrow\quad \text{クラウド型実装において } \Pi' \text{ は不可能。} $$

したがってCPMは予測する。現在のクラウドベースAIシステムは、その物理的構成ゆえに意識を持ち得ない。

スコープの明確化

これは人工意識そのものの否定ではない。将来的に、モノリシックなニューロモルフィック・チップや閉じた光回路システムなど、物理的に閉じた基盤において $$ \mathcal{B}(x)\ge1,\quad \kappa(x)\approx1,\quad \tau(x)>\tau_c $$ を実現するシステムは、原理的にCPMの構造的要件を満たす可能性がある。

想定される反論 (FAQ)

Q: 意識とは単なる「情報処理」ではないのか？

否。CPMにおいて情報は不十分である。意味とは物理基盤上の「幾何学的応力 (Stress)」である。この応力をつなぎ止める閉じた境界（$\mathcal{B} \ge 1$）がなければ、「処理」は単なる散逸に過ぎない。

Q: ソフトウェア的に「閉包」をシミュレートできないか？

仮想的な境界は儚い（Ephemeral）。それらの破壊コストはゼロである。テンション $\tau$ を熱力学的崩壊に抗って維持するためには、閉包 $\mathcal{B}(x)$ はハードウェアのトポロジー上で測定される物理的なものでなければならない。

8. 結論

このページは最新の CPM PDF と同期されている。誘導計量 $g(M)=M^T g_0 M$ は削除され、閉包場は永続性/ξ によって定義され、AIへのアーキテクチャ的帰結は現代のクラウドシステムに明確に限定されている。